a) Oui, par exemple =-x^2+4)
b) On a :
-P(1)=9-7)
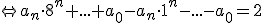
\cdot k=2) (car (car \cdot l) où où 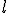 se compose de termes en se compose de termes en 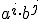 ) )
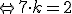 Or, Or,  étant entier (car les termes du polynôme le sont), ceci est impossible. étant entier (car les termes du polynôme le sont), ceci est impossible.
La réponse est donc non!
c) Avec le même argument que précédemment, on trouve que 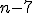 et donc et donc 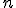 doivent être divisibles par 7. Montrons que cette condition nécessaire est suffisante. doivent être divisibles par 7. Montrons que cette condition nécessaire est suffisante.
Le polynôme défini par =7+(\frac{n}{7}-1)\cdot (x-1)) vérifie vérifie =7) et et =n) et ses termes sont entiers ssi et ses termes sont entiers ssi 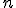 est divisible par 7, ce qui représente la condition nécessaire et suffisante. est divisible par 7, ce qui représente la condition nécessaire et suffisante. |


